|
AN "OPEN AIR UNIVERSITY" FOR TEACHING INITIATE STUDENTS THE SCIENTIFIC ARTS OF ASTRONOMY & NAVIGATION
 THE REASON FOR THE NAZCA LINES. Everywhere that the ancient European-Mediterranean cousin nations sailed to and set up permanent civilisations, they religiously recorded their sciences into the landscape and public buildings by way of specially chosen lengths and angles. These repositories of knowledge were for permanent, ongoing reference, such that the imperative mathematics and numerical values associated with "civilisation" could never be lost. Moreover, the special knowledge had to be handed on fully intact to each ensuing generation. To neglect this duty was to doom one's offspring, wherein there was a very real threat that they could lose grasp of "civilisation" and the abundance associated with a fully optimised society that had the best possible chance of survival. Under the normal modus operandi used in most regions of Europe and the Mediterranean, a central hubstone was placed into the landscape and then a series of outer marker stones placed as satellites set to specific distances and angles from the central hub. The inbuilt scientific principles of these "standing stone circle" or other arrangements of markers could then be extracted by use of an accurate rule to measure the length between markers. Secondary codes could be extracted by a theodolite-compass that gave a reading around from due north and produced a significant number in the process. The values produced related to such things as the equatorial circumference of the earth or periods of duration in cyclic astronomy. As a location for marking terrain with geometry and creating a huge "open air university", Nazca was unique. There was an abundance of water, due to the sprawling Andes mountain catchments area inland, which fed large fertile pockets of farmland in the Nazca desert. Despite this abundance of subterranean water, the desert surface itself was one of the driest, most static and sterile environments on Earth, which virtually never saw any rain or disturbance-shifting of the surface layer. The desert was strewn with reasonable small, manageable but dark stones and once these were removed and a shallow excavation undertaken, the sub-strata exposed was chalky-white and contrasted vividly with the natural surface. This unique and rare quality meant that whole geometric shapes could be permanently etched or tattooed into the desert, rather than employing the usual method of creating imaginary lines between stone markers. There has been no significant rain at Nazca since the last ice-age and any marking of the desert surface will yet endure for potentially thousands of years, as long as each ensuing generation respects and preserves undisturbed the landscape geometric patterns and masterfully executed glyphs. The special knowledge that ancient civilisations need to preserve included: 1. Several systems, based upon different number families, that more than adequately described the equatorial circumference of the Earth and how to grid reference it for safe traversal. By each of these systems it was possible to cross the great oceans and do accurate positional plotting throughout the entire journey, ensuring safe arrival at a distant destination. 2. Inasmuch as the moon is the greatest determinant of the weather, due to the extreme gravitational pull and influence it has on our atmosphere, it was imperative to know the short and longterm cycles of the moon. The movements and daily progress of the moon was monitored, not only through the month and lunar year, but throughout the entire 18.613-year lunar nutation cycle. 3. For ordered and abundant society, crops had to be planted and harvested on time. This required an accurate calendar system that followed the sun and the moon simultaneously (lunisolar). For this the ancient cousin nations used the ages-old Sabbatical Calendar system, which was fashioned around 7-solar years (2556.75-days) working in conjunction with 7.2-lunar years (2551.5-days). In ancient Europe, the mistletoe culling ceremony, which occurred on the sixth day after the solar count commenced, was for initiating the lunar count, such that both periods would terminate on the same day 7-solar years later. THE GIZEH PLATEAU OF EGYPT ... BUREAU OF STANDARDS FOR THE MOBILISED AND SCATTERED EUROPEAN NATIONS. In mathematically assessing the lengths and angles of geometric earthmound complexes (like the Octagon of Newark, Ohio) or stepped pyramids and standing stone marker systems on various continents, it is unsurprising to find that the selfsame lengths and angles (or greater & lesser ratio expressions of the standard values) are represented on sites around the world. The mathematical fingerprints of the cousin European nations are encoded wherever these highly mobilised people set up long enduring mining operations, colonies or longterm civilisations (like at Teohuanacan, Mexico or Tiahuanaco in Bolivia). It is worthy to note that all of the cubits, feet or other lengths, volumes and weights in popular use within one cousin nation were in direct ratio to the standards of another cousin nation. This attribute of all of the standards being based upon the selfsame integrated parcel of factorable numbers facilitated trade in and around the ancient Mediterranean or Atlantic seabord and the dispensing of correctly weighed-out quantities or precise volumes at all the marketplaces. The Central Bureau of Standards was, for centuries or millenniums, amidst the edifices and everywhere-represented coded attributes of the Gizeh Plateau of Egypt. The most prominent coded structures on the plateau were the Great Pyramid, which carried (primarily) codes to do with the equatorial size of the Earth, and the Khafre Pyramid, which carried codes to do with the cycles of the moon and the 3,4,5 triangle. Here, in part, is what these two structures did: THE GREAT PYRAMID 1. Its length per side was coded to be 756 feet of 12-inches each. This equated to 72 Hebrew reeds, 360 Assyrian cubits, 432 Hebrew Royal cubits, 437.5 large Egyptian Royal cubits, 440 standard Egyptian Royal cubits, 540 Hebrew "cubits of a man", 720 Greek feet or 777.6 Roman feet, etc. 2. Two full circumnavigations of the Great Pyramid equated to 6048-feet, which was called 1-minute of Earth equatorial arc. In other words, 6048-feet X 60 = 1-degree of arc and 1-degree X 360 = the entire distance around the world at the equator. By the Great Pyramid's standard the Earth was 12 X 12 X 12 X 12 X 1.2 Greek miles of 5250-feet (of 12-inches each) in circumference or 24883.2 Greek miles. THE KHAFRE PYRAMID 1. The Khafre Pyramid was 15/16ths the length of the Great Pyramid or 708.75-feet per side. Half of 708.75-feet is 354.375-feet and that value, in days, happens to be the duration of the lunar year. 2. The Khafre Pyramid was built to the 3,4,5 formula used by carpenters and engineers since time immemorial, so half its base length was 3 X 118.125-feet (in days this would be 4 lunar months), its vertical height was 4 X 118.125-feet and its side diagonal face length was 5 X 118.125-feet. With these simple examples of coding from the Gizeh Plateau of Egypt, let's now show how this selfsame coding was indelibly encrypted into the Nazca desert and how the Nazca geometry was utilised to teach initiate students principles of astronomy and navigation. On the 21st of December 2007, Gary Vey of Viewzone wrote the following suggestions and requests to this researcher as the basis for an article: 'I'd suggest that you take one set of lines and angles and explain them. I'd also like to imagine how this nautical school worked, for example, for a novice sailor or navigator. Did they walk the lines with a compass or using the stars? How do you envision this area being used?' ANALYSIS OF A RANDOMLY CHOSEN GEOMETRIC PATTERN AT NAZCA, PERU.  A simple trapezoid, with lines running through it stretches on a diagonal across the Nazca desert. Let's decipher some of its coded attributes, using the well-known, well-worn measurement standards of the ancient Mediterranean and Egypt, which survived in greater or lesser ratio form in all of the measurement standards of European countries before metrification. 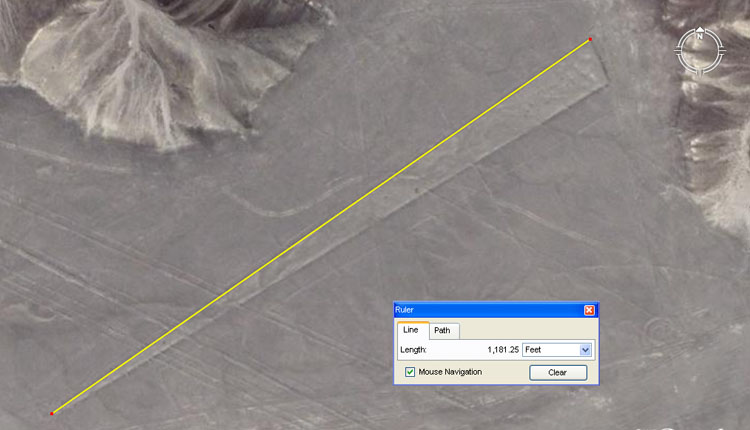 The Google Earth Ruler fairly represents the length of this line as 1181.25-feet. Didn't we just discuss the basic unit of length used to create the Khafre Pyramid 3,4,5 triangle as 118.125-feet, which in days would be 4 lunar months? Let's try another side of the trapezoid. 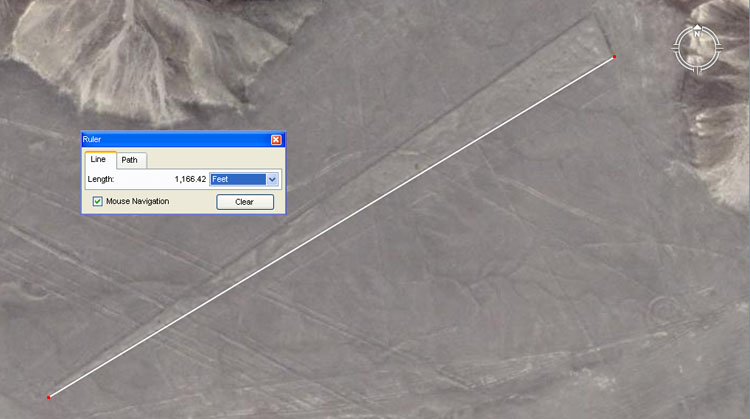 This side of the trapezoid equates fluidly to 1166.4-feet or 1200 Roman feet of 11.664-inches each. Like the Egyptians, who had 3 virtually undetectable variations in Royal cubits, the Romans had two renditions of the foot; one at 11.664-inches (lunar foot) and another at 11.6666-inches (or 11 & 2/3rds ... overland pace foot). It must be recognised by the researcher that all of the ancient cousin nations were using all of the various standards and that expressions of such things as the Greek stadia occur in the dimensions of Stonehenge, a couple of thousand years before there was a Greek civilisation. Let's now analyse a slightly larger sample. 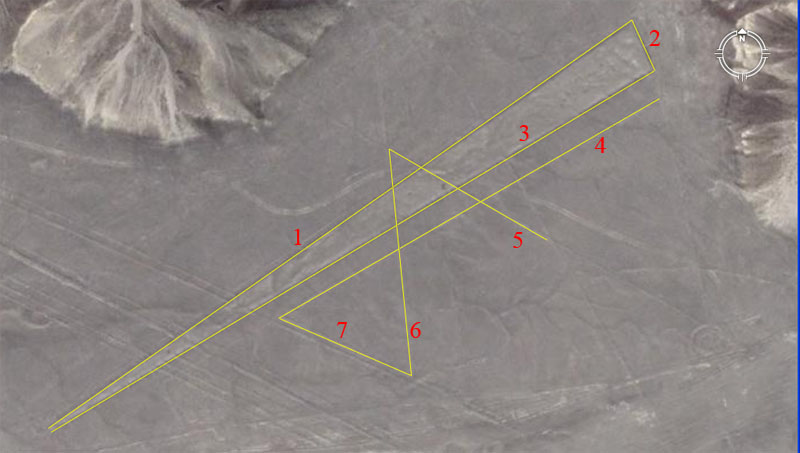 As with each pattern at Nazca, there are multiples of codes associated with each length and these are marked by individual stations. In this instance, however, we'll only identify the overall length codes and angles, which are: 1. The length is 1181.25-feet and the angle is 55-degrees (to a tolerance of less than .15 of a degree). The length carries a lunar code and 118.125-days would be 4-lunar months (to a tolerance of about 3.5 minutes). The degree angle is in homage to the "11" series or family of values. The British league (3.125-miles), mile (5280-feet), furlong or furrowlong (660-feet), chain (66-feet), rod or perch (16.5-feet), fathom (originally 5.5-feet) and link (7.92-inches), were based upon this series. The ancient Germans and Scandinavians also used "11" series values for navigation. The Great Pyramid also symbolically codes this navigational method, by reading its length as 756.25-feet instead of 756-feet. 2. The length coding appears to be 92.16-feet (92 & 4/25ths) and the angle is 155.52-degrees (155 & 13/25ths). Under the great Pyramid's reading of the equatorial circumference of the Earth as 12 X 12 X 12 X 12 X 1.2 (so-called Greek) miles of 5250-feet each, the sum of 92.16-miles would be 1/270th of the equatorial circumference. The degree angle is also a navigational value that relates directly to the equatorial circumference of the Earth and 155.52-miles would be 160th of the circumference. Note: the value of 155.52 is half of 311.04 and this value was very prevalent in ancient Mediterranean volume capacities. For example:
3. The length is 1166.4-feet and the angle is 59.0625-degrees (59 & 1/16th). The length is simply 1200 (so-called Roman) lunar feet of 11.664-inches each or 1200 overland feet of 11.6666-inches (11 & 2/3rds). Again, this value recurs in the ancient volumes of the Mediterranean:
The angle in this instance is 59.0625-degrees and this coding is lunar. The sum of 59.0625-days would be 2 lunar months to a tolerance of about 1.7-minutes. It will be recalled that the Khafre Pyramid was built to a 3,4,5 triangle method in which the base increment was 118.125-feet. Therefore, half the base length was 354.375-feet, which in days is a lunar year; the vertical height was 472.5-feet and the side diagonal length was 590.625-feet. 4. The distance is 729-feet and the angle is 240-degrees / 60-degrees. This length is lunar coding and 729-feet would equate to 750 Roman feet or 150 Roman Paces of 58.32-inches each. The same length would equate to 450 ancient Swedish Alns (19.44-inches), which is also known as the "Rydaholmsalm" (a prototype of which was once kept in the church of Rydaholm, Smäland). The Bush Barrow Lozenge artefact from Stonehenge has a design length of 7.29-inches or 1/8th of a Roman Pace. It was fabricated a couple of thousand years before there was a Roman Empire of any consequence. The angle in this instance is just an expression of 360-degrees, with 240 being 2/3rds of 360 or 60 being 1/6th. 5. The distance is 302.4-feet and the angle is 120-degrees / 300-degrees.< The Great Pyramid is 756-feet per side or 1/2 a minute of equatorial arc for one circumnavigation. The sum of 302.4-feet would equate to 3-seconds of Earth equatorial arc under the Great Pyramid's assignment. The angle of 120-degrees is yet another expression of 360-degrees. 6. The distance is 378-feet and the angle is 354.375-degrees. The length of 378-feet is one half the length of the Great Pyramid. The angle of 354.375-degrees is in homage to the 354.375-days in a lunar year. 7. The distance is 240-feet and the angle is 113.4-degrees. The distance of 240-feet is, again, in homage to the 360-degree system. It would also seem obligatory that this line would also have been pegged to indicate 243-feet, which is a strong lunar code. The angle of 113.4-degrees is strong lunar coding and there would be 60-periods of 113.4-days in the 6804-day lunar nutation cycle. There would be 22.5-periods of 113.4-days in the 7.2-lunar year count monitored within the lunisolar Sabbatical Calendar system. The width of the Station Stone's rectangle at Stonehenge is 113.4-feet. Greek Historian Herodotus was told by Egyptian priests that one of the ways of reading the length of the Great Pyramid was in 800 increments. This would infer a ruler of 11.34-inches. The value of 3-sides of the Great Pyramid is 2268-feet or 1134-feet X 2, etc. Essentially, taking readings of the base dimensions of the Great Pyramid with a rule of 11.34-inches meant that in-built lunar codes could be extracted. HOW DID THE NAZCA "NAUTICAL SCHOOL" WORK? Long before a prospective navigator is entrusted with the safety of a ship, its crew and precious cargo, there has to be a period of intensive training on land to prepare one for the rigours and dangers of the open sea. Julius Caesar, in speaking of the British schools stated: "They also lecture on the stars in their motion, the magnitude of the Earth and its divisions..."  Left: The Great sprawling school
of Avebury Henge in Southern England, which provided tutorials in navigation
and astronomy, not only internally, but from stations and structures in the
surrounding landscape that related back to a giant obelisk within the henge.
The same lengths and angles that one finds on the Gizeh Plateau of Egypt are
represented in the tutorials of Avebury Henge. The circumnavigating embankment
acted as a false horizon, similar to the horizon on the open sea and students
could familiarise themselves, over a long period of training, with solar,
lunar, planetary and stellar rises and sets or cycles. Initiate students could stand and work from marked positions within the henge and earth embankment complexes of antiquity in a manner similar to standing at the helm of a ship. From this position they could carefully observe the rising and alighting positions of stars, as well as the order, timing or offset positions of the rises and sets. By gazing into the north, they could observe the swirling action of stars in that quarter and how some never fully set. They could determine that a particular northern star at the centre of the swirl or a dark pocket adjacent gave a reading of true north. During the course of the year they would observe how the sun rose through a changing background of stars as the Earth made its annual journey around the sun. They learned from intense observation how to accurately determine the dates of the equinoxes and solstices. They learned how to determine latitude with good relative accuracy by the use of "shadow poles." Songs and mnemonic chants were used to remember the positions of zenith bright stars and the regions of the Earth they moved to and hovered above during the calendar year. These zenith bright stars helped to determine longitude for navigators at sea. Researcher, Gene Matlock mentions one of the surviving Hindu navigational chants as saying: 'When the sun rises in Jambudv’pa, it is the middle watch of the night in Aparagoyana; sunset in Aparagoyana is midnight in Jambud’pa, and sunrise is noon in Jambud’pa, sunset in Pubbavideha and midnight in Uttara Kuru.' Or as Julius Caesar said concerning the schools of Britain: '... in the schools of the Druids they learn by heart a great number of verses ...'Many of these poems or chants would have related to stellar positions, such that navigators could reorientate themselves and recalculate positions after extended periods of buffeting storms had obscured view of the celestial map. Beyond an intricate knowledge of celestial movements, cycles or important stellar groupings, like the twelve constellations of the ecliptic, the student had to learn the art of determining accurate degree angles off true north. This was imperative knowledge that would have required a huge amount of practice to achieve. It was essential to gain this ability due to the demands of steering sailing ships accurately across the wide, featureless oceans, while being forever at the mercy of the wind. Because of the prevailing wind direction, or its ability to change at any given moment, voyages were a series of zigzag legs to a destination. The ship could tack on the wind only so far during a leg of travel and would then be required to come about and tack on another angle in order to stay on course to the destination. At all times, the navigator had to keep track of the ship's position at sea and accurately plot the ship's progress on a navigational chart or slate. It is exactly for this reason that we have very strange number values to describe a Greek mile as 5250-feet, a British mile of 5280-feet or a Roman mile of 4860-feet, etc. These "miles" of antiquity were "windows of mathematical opportunity" that worked with the complex formula of PI (3.1416) ... used for turning a linear leg of ship's travel across the ocean into a circle from which accurate degree angles to the destination could be calculated. A simple "mile" of 5000-feet would not have worked with PI.
The ancient cousin nations had lesser known increments called "pygons", etc., that worked within 360-degree circles or other circle calibrations to deliver up accurate degree angles when doing positional plotting at sea. In order for the system to work accurately, the helmsman had to maintain a known degree angle heading until a certain number of full "miles" or "leagues" were completed. The experienced navigator could determine boat speed with good relative accuracy from the tension of the sails or the riding height of the hull and the way the ship was planing on the water. Using a knotted rope tied to a bucket that was cast overboard aft, the navigator could time the speed at which the rope played out and calculate the number of "knots" the ship was traveling. Devices like "sand clocks" aided in these types of calculations. By being ever alert and doing constant mental arithmetic the navigator could know, with good relative accuracy when the chosen distance for a leg was nearing completion and it was necessary to come about. The selfsame landscape geometry found from Egypt to Europe to the Americas to New Zealand demonstrates advanced knowledge of navigational methods and the ability to grid reference the globe for safe traversal ... or as Julius Caesar stated: 'the magnitude of the Earth and its divisions...' At Nazca, each design pattern contained tutorials by way of length and angle. The values incorporated as a teaching aid in one generation could be forevermore extracted by later students using an accurate measuring rule or manual theodolite-compass. Once the values were extracted anew, it would become the duty of the teacher (Master of the Craft) to explain the significance of the values and the duty of the student to commit that knowledge to memory. All values incorporated, with exception to the unresolvable numbers for PI (3.1459...) and PHI (1.6180339...) were "factorable" numbers that worked in mathematical progressions. The progressions, which related to the different navigational methods or astronomical cycles, could be calculated from a base value using abacus or quippu (string-knot) devices. The quippu's were also used for permanent storage of the special numbers, some of which would, undoubtedly, have been SINE values used in overland trigonometry for doing distance calculations from an established, surveyor's baseline. The distribution of these "string-knot" devices ranged all the way to ancient New Zealand, where they were called "kupu" in the Maori language; a name derived from the earlier "uru-kehu" (reddish, golden-tinged hair) & "kiri-puwhero" (reddish, light-complexion skin) Turehu people, who left their "marker systems" all over the New Zealand landscape. Many of these former inhabitants were "Viracochas" (sea-foam people) who escaped from South America and fled to the islands of the Pacific, taking their South American cultural expressions and food plants with them. DESIGN & BUILD TUTORIALS; INTERPRETIVE TUTORIALS; LEARNING LENGTH & ANGLE CODES BY ROTE & REPETITION There has been much discussion about the fact that the giant glyphs of hummingbirds or other species of birds, mammals or a spider can only be seen from the air, but are difficult to visualise and identify from ground level. However, in learning to read exact coded measurements and accurately determine degree angles, each giant glyph represented a dynamic resource for hands on practice and problem solving. One generation or group of students and their masters could devise an intriguing design groundplan that incorporated many coded aspects, then etch it into the terrain to act as a repository of extractible information and an added tutorial for the school. Future students would be assigned the task of standing in the midst of the "hard to visualise" design and, over a day or two, through recording the precise measurements and angle determinations, recommit the design to parchment, papyrus or slate as a very recognisable object. The students would then be required to interpret the multiple meanings found in lengths, breadths and degree-angle orientations that had been deliberately incorporated into the design... and commit the encoded scientific principles to memory. On the larger Nazca rectangles, with their cairn benchmark hubs, lines extended out on specific angles to other geometric patterns further afield. Also, each of the utterly abstract geometric designs at Nazca was loaded with internal and external stations, each containing differing length and angle codes. Students assigned to work within a pattern would have been equipt with surveying devices, such as measuring ropes and theodolites. It should be mentioned that the use of loadstone to make simple magnetic compasses had been known since remote antiquity. One method was to fasten a small elongated sliver of loadstone to a piece of buoyant wood, floating in a bowl of water. The wooden float would then orientate itself to magnetic north and the simple addition of less than 20-degrees would indicate true north with good relative accuracy. Such devices could be used on cloudy days to stay on course at sea. After first determining true north from a benchmark station at Nazca, all of the in-built codes of a huge geometric pattern under study could be systematically extracted one by one. After years of intensive training at these land based schools, the art of accurately fixing onto and maintaining a chosen heading of travel or calculating distances covered for each leg, would have become second nature. Should lengthy buffeting storms arise at sea, resulting in disorientation and some loss of knowledge as to exact position, the highly trained navigator would have been very adept at reading the stellar map overhead, resulting in the restoration of knowledge pertaining to the ship's position. By then undertaking angle calculations and creating a navigational plan, the journey to a safe haven could recommence anew. STALEMATE AND STALLED-SCHOLARSHIP AT NAZCA There have been years of speculation and sensationalism concerning the Nazca lines, but very little realistic scholarship and proper groundwork that would lead to positively solving the mystery. As it turns out, the problem isn't that complex, as Nazca is simply ground based geometry of very measurable dimensions and angles. All that is required is proper surveying, with the subsequent results being subjected to comprehensive comparative-analysis on computers. Many genuine scholars are frustrated by the "foot-dragging" of the Peruvian government and a recent Chicago Tribune article complained about "shortcomings" in Nazca scholarship. And it raised new questions about the Peruvian government's commitment to sophisticated scientific scholarship.
There is no central catalogue detailing the hundreds of lines and figures already
mapped and measured. There is no database for archeologists or, for that matter,
a team headed by a literature professor from Yamagata University in Japan, to
refer to when trying to piece together the history of the Nazca. ... the National
Institute of Culture has no central registry of the geoglyphs."
"The government should open its doors and say that all the scientists of
the world, all the foundations, are invited to come and work," Lancho said.
"But the Peruvian government puts up too many obstacles to projects. One example is the painstaking excavation of the Cahuachi complex, the Nazca's ceremonial and administrative center. Though Orefici's team has gathered a treasure of artifacts and a wealth of knowledge amid its pyramids and esplanade, Cahuachi is little noticed outside select archeological circles." (Source: Chicago Tribune by Colin McMahon, May 24, 2006). For many years now, Nazca and its history has increasingly fallen under the control of "social-engineers" and any actual truth about the region and it's former high civilisation is conspicuous by its absence. Scholarship in that quarter is, quite-frankly, abysmal, to the extent that the physical anthropology of the tens of thousands of perfectly preserved (line-builder) mummies exhumed in the region remains a well-guarded secret from the general public ... as also with the Mediterranean-European measurement standards used in the layout of the lines and glyphs that cover the Pampa. A similar dearth of knowledge afflicts the flow of dimensional, artefact or physiological information about mummies found within the Cahuachi pyramid complex, which sits adjacent to the Nazca desert geometry. The "Stone Balls of Costa Rica" were yet another example of an overland marker system used to teach navigation... but one that could work in a lush, wet environment, as opposed to a stark, arid desert. Martin Doutré, New Zealand, December 25th 2007. © British Standard spelling. For more comprehensive analysis of the Nazca geometry CLICK HERE
Comments: | ||||
